Práctica: Evaluación de Modelos Logísticos y Cross-Validation

Author

SOC3070 · Mauricio Bucca

Published

October 13, 2025

1. Contexto y objetivos

Evaluar el desempeño predictivo de un modelo logístico con cross-validation.

2. Cargar y preparar los datos

#> Rows: 601
#> Columns: 10
#> $ sex          <fct> male, female, female, male, male, female, female, male, f…
#> $ age          <dbl> 37, 27, 32, 57, 22, 32, 22, 57, 32, 22, 37, 27, 47, 22, 2…
#> $ ym           <dbl> 10.00, 4.00, 15.00, 15.00, 0.75, 1.50, 0.75, 15.00, 15.00…
#> $ child        <fct> no, no, yes, yes, no, no, no, yes, yes, no, yes, yes, yes…
#> $ religious    <int> 3, 4, 1, 5, 2, 2, 2, 2, 4, 4, 2, 4, 5, 2, 4, 1, 2, 3, 2, …
#> $ education    <dbl> 18, 14, 12, 18, 17, 17, 12, 14, 16, 14, 20, 18, 17, 17, 1…
#> $ occupation   <int> 7, 6, 1, 6, 6, 5, 1, 4, 1, 4, 7, 6, 6, 5, 5, 5, 4, 5, 5, …
#> $ rate         <int> 4, 4, 4, 5, 3, 5, 3, 4, 2, 5, 2, 4, 4, 4, 4, 5, 3, 4, 5, …
#> $ nbaffairs    <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
#> $ everaffair_d <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…

3. Dos modelos de distinta complejidad

#>                Estimate Std. Error
#> (Intercept)  0.15392342 0.42235014
#> ym           0.02151079 0.02128940
#> childyes     0.40748669 0.28317859
#> rate        -0.46156942 0.08716552

#>                            Estimate Std. Error
#> (Intercept)           -1.3925777289 2.05687210
#> childyes               1.7514867807 2.74367721
#> ym                     0.6167620791 0.80395121
#> rate                  -0.3731941944 0.48830584
#> I(ym^2)               -0.0293627976 0.04802184
#> childyes:ym           -0.3988596835 0.92275917
#> childyes:rate          0.0235002356 0.66708392
#> ym:rate               -0.0156919830 0.19187077
#> childyes:I(ym^2)       0.0156403201 0.05338503
#> rate:I(ym^2)          -0.0001854899 0.01168887
#> childyes:ym:rate      -0.0438745025 0.22409015
#> childyes:rate:I(ym^2)  0.0039896771 0.01315239

4. Evaluación in-sample: AIC y BIC

#> # A tibble: 2 × 3
#>   Modelo                                                      AIC   BIC
#>   <chr>                                                     <dbl> <dbl>
#> 1 everaffair_d ~ ym + child + rate                          639.8 657.4
#> 2 everaffair_d ~ child * ym * rate + child * I(ym^2) * rate 644.5 697.3

5. Limitación: posible overfitting

Usamos cross-validation para evaluar fuera de muestra.

6. Cross-validation con caret

Code

> ctrl <- trainControl(
+   method = "repeatedcv",
+   number = 10,
+   savePredictions = TRUE,
+   classProbs = TRUE,
+   summaryFunction = twoClassSummary
+ )
> 
> set.seed(123)
> 
> cv_m0 <- train(
+   everaffair_d ~ ym + child + rate,
+   data = affairs, method = "glm",
+   family = "binomial", trControl = ctrl,
+   metric = "ROC"
+ )
> 
> cv_m1 <- train(
+   everaffair_d ~ child * ym * rate + child * I(ym^2) * rate,
+   data = affairs, method = "glm",
+   family = "binomial", trControl = ctrl,
+   metric = "ROC"
+ )

7. Resultados del cross-validation

Code

> cv_m0$results

#>   parameter       ROC      Sens Spec      ROCSD     SensSD     SpecSD
#> 1      none 0.6719936 0.9667633 0.08 0.09216978 0.03810189 0.06885304

Code

> cv_m1$results

#>   parameter       ROC      Sens Spec      ROCSD     SensSD     SpecSD
#> 1      none 0.6592351 0.9556522  0.1 0.06527264 0.03474516 0.07200823

8. Matrices de confusión promedio

Code

> confusionMatrix(cv_m0)

#> Cross-Validated (10 fold, repeated 1 times) Confusion Matrix 
#> 
#> (entries are percentual average cell counts across resamples)
#>  
#>           Reference
#> Prediction   no  yes
#>        no  72.5 23.0
#>        yes  2.5  2.0
#>                             
#>  Accuracy (average) : 0.7454

Code

> confusionMatrix(cv_m1)

#> Cross-Validated (10 fold, repeated 1 times) Confusion Matrix 
#> 
#> (entries are percentual average cell counts across resamples)
#>  
#>           Reference
#> Prediction   no  yes
#>        no  71.7 22.5
#>        yes  3.3  2.5
#>                             
#>  Accuracy (average) : 0.7421

9. Visualización del desempeño cruzado

Code

> resamps <- resamples(list(Simple = cv_m0, Complejo = cv_m1))
> bwplot(resamps, metric = "ROC", main = "Comparación de desempeño (10-fold CV)")

Code

> cv_compare <- bind_rows(
+   cv_m0$resample %>% mutate(modelo = "Simple"),
+   cv_m1$resample %>% mutate(modelo = "Complejo")
+ )
> 
> ggplot(cv_compare, aes(x = modelo, y = ROC, fill = modelo)) +
+   geom_boxplot(alpha = 0.7) +
+   scale_fill_manual(values = c(julia$coral, julia$teal)) +
+   labs(
+     title = "Desempeño en validación cruzada",
+     subtitle = "Comparación del área bajo la curva (ROC)",
+     x = "", y = "ROC promedio"
+   ) +
+   theme_julia()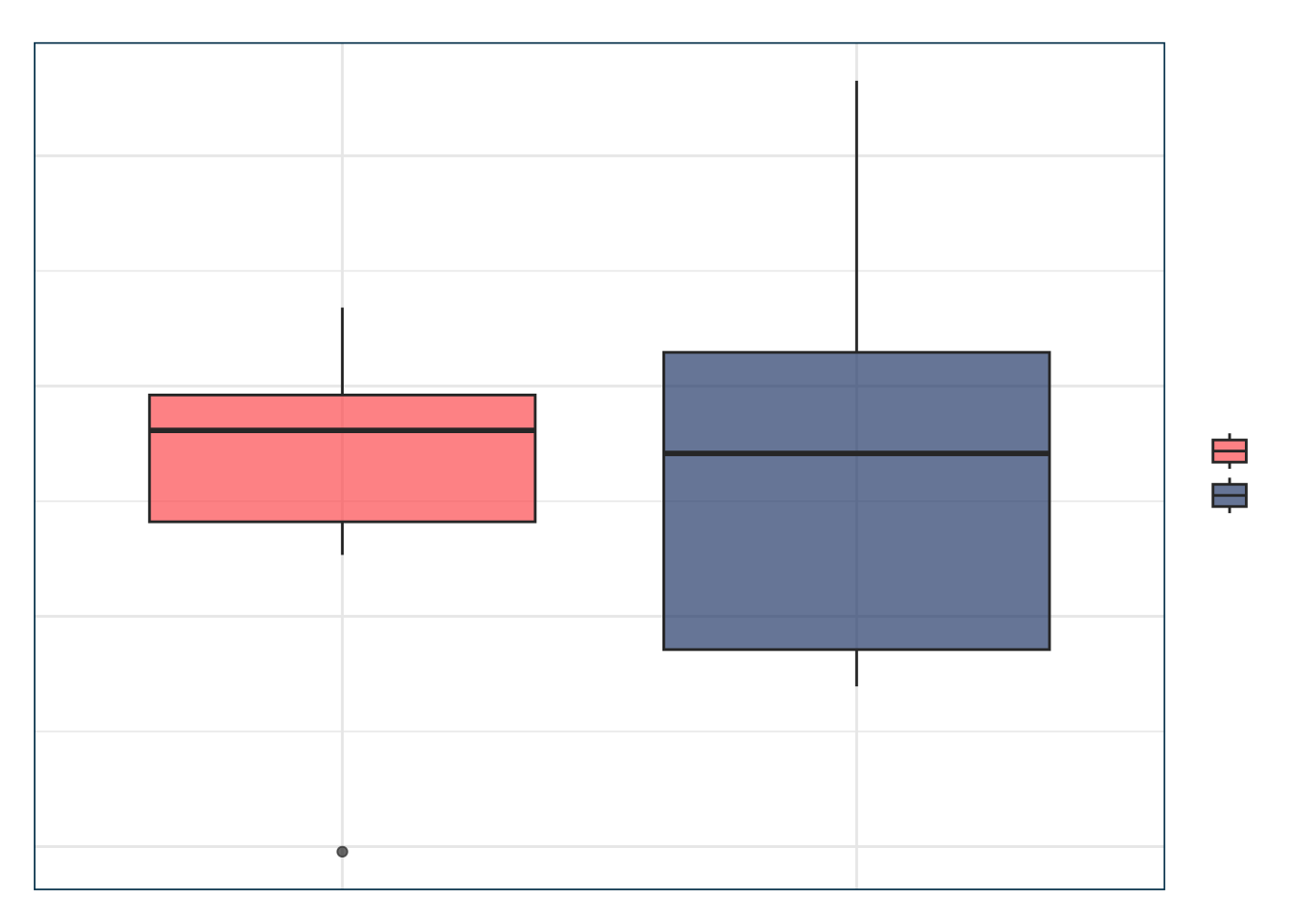

10. Conclusión

Cross-validation permite estimar error fuera de muestra y evitar sobreajuste. En regresión logística, guía la selección de modelos con verdadero poder clasificador.