SOC3070 Análisis de Datos Categóricos

Author

Tarea corta 4

Ponderación: 6% de la nota final del curso.

Datos:

En esta tarea trabajaremos con el dataset Spambase disponible en el repositorio UCI: https://archive.ics.uci.edu/dataset/94/spambase

Este dataset contiene 4.601 correos electrónicos, de los cuales aproximadamente el 40% son spam. Cada observación corresponde a un email y las variables predictoras son 57 características precomputadas que incluyen:

Frecuencia relativa de palabras como “free”, “money”, etc.
Frecuencia de caracteres como ;, (, [.
Longitud de secuencias de mayúsculas.

El objetivo es clasificar correos como spam (1) o no-spam (0).

#> Rows: 4,601
#> Columns: 58
#> $ word_freq_make             <dbl> 0.00, 0.21, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_address          <dbl> 0.64, 0.28, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_all              <dbl> 0.64, 0.50, 0.71, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_3d               <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_our              <dbl> 0.32, 0.14, 1.23, 0.63, 0.63, 1.85, 1.92, 1…
#> $ word_freq_over             <dbl> 0.00, 0.28, 0.19, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_remove           <dbl> 0.00, 0.21, 0.19, 0.31, 0.31, 0.00, 0.00, 0…
#> $ word_freq_internet         <dbl> 0.00, 0.07, 0.12, 0.63, 0.63, 1.85, 0.00, 1…
#> $ word_freq_order            <dbl> 0.00, 0.00, 0.64, 0.31, 0.31, 0.00, 0.00, 0…
#> $ word_freq_mail             <dbl> 0.00, 0.94, 0.25, 0.63, 0.63, 0.00, 0.64, 0…
#> $ word_freq_receive          <dbl> 0.00, 0.21, 0.38, 0.31, 0.31, 0.00, 0.96, 0…
#> $ word_freq_will             <dbl> 0.64, 0.79, 0.45, 0.31, 0.31, 0.00, 1.28, 0…
#> $ word_freq_people           <dbl> 0.00, 0.65, 0.12, 0.31, 0.31, 0.00, 0.00, 0…
#> $ word_freq_report           <dbl> 0.00, 0.21, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_addresses        <dbl> 0.00, 0.14, 1.75, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_free             <dbl> 0.32, 0.14, 0.06, 0.31, 0.31, 0.00, 0.96, 0…
#> $ word_freq_business         <dbl> 0.00, 0.07, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_email            <dbl> 1.29, 0.28, 1.03, 0.00, 0.00, 0.00, 0.32, 0…
#> $ word_freq_you              <dbl> 1.93, 3.47, 1.36, 3.18, 3.18, 0.00, 3.85, 0…
#> $ word_freq_credit           <dbl> 0.00, 0.00, 0.32, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_your             <dbl> 0.96, 1.59, 0.51, 0.31, 0.31, 0.00, 0.64, 0…
#> $ word_freq_font             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_000              <dbl> 0.00, 0.43, 1.16, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_money            <dbl> 0.00, 0.43, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_hp               <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_hpl              <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_george           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_650              <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_lab              <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_labs             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_telnet           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_857              <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_data             <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_415              <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_85               <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_technology       <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_1999             <dbl> 0.00, 0.07, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_parts            <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_pm               <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_direct           <dbl> 0.00, 0.00, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_cs               <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_meeting          <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_original         <dbl> 0.00, 0.00, 0.12, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_project          <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_re               <dbl> 0.00, 0.00, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_edu              <dbl> 0.00, 0.00, 0.06, 0.00, 0.00, 0.00, 0.00, 0…
#> $ word_freq_table            <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ word_freq_conference       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ char_freq_semicolon        <dbl> 0.000, 0.000, 0.010, 0.000, 0.000, 0.000, 0…
#> $ char_freq_paren            <dbl> 0.000, 0.132, 0.143, 0.137, 0.135, 0.223, 0…
#> $ char_freq_bracket          <dbl> 0.000, 0.000, 0.000, 0.000, 0.000, 0.000, 0…
#> $ char_freq_exc              <dbl> 0.778, 0.372, 0.276, 0.137, 0.135, 0.000, 0…
#> $ char_freq_dollar           <dbl> 0.000, 0.180, 0.184, 0.000, 0.000, 0.000, 0…
#> $ char_freq_hash             <dbl> 0.000, 0.048, 0.010, 0.000, 0.000, 0.000, 0…
#> $ capital_run_length_average <dbl> 3.756, 5.114, 9.821, 3.537, 3.537, 3.000, 1…
#> $ capital_run_length_longest <int> 61, 101, 485, 40, 40, 15, 4, 11, 445, 43, 6…
#> $ capital_run_length_total   <int> 278, 1028, 2259, 191, 191, 54, 112, 49, 125…
#> $ spam                       <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…

Tareas

Ajusta dos modelos de regresión logística para predecir correos spam:
- Modelo 1 (parsimonioso / sustantivo): utiliza un pequeño conjunto de variables plausibles, por ejemplo word_freq_free (frecuencia de la palabra free), char_freq_exc (frecuencia del signo “!”) y capital_run_length_average (longitud promedio de secuencias en mayúsculas).
- Modelo 2 (completo): incluye todas las variables disponibles en el dataset.

> # Modelo 1: parsimonioso con variables sustantivas
> m1 <- glm(spam ~ word_freq_free + word_freq_money + char_freq_exc +
+             capital_run_length_average, data = spam, family = binomial)
> 
> # Modelo 2: completo con todas las variables
> m2 <- glm(spam ~ ., data = spam, family = binomial)

Para cada modelo, calcula las probabilidades predichas de ser spam para cada correo electrónico.

> p1 <- predict(m1, type = "response")
> p2 <- predict(m2, type = "response")

Calcula manualmente el log-loss promedio de cada modelo.

> logloss <- function(y, p) {
+   -mean(y * log(p) + (1 - y) * log(1 - p))
+ }
> 
> ll1 <- logloss(spam$spam, p1); print(ll1)

#> [1] 0.4764308

> ll2 <- logloss(spam$spam, p2); print(ll2)

#> [1] 0.1973229

Grafica la curva ROC y calcula el AUC para ambos modelos.

> roc1 <- roc(spam$spam, p1); plot(roc1)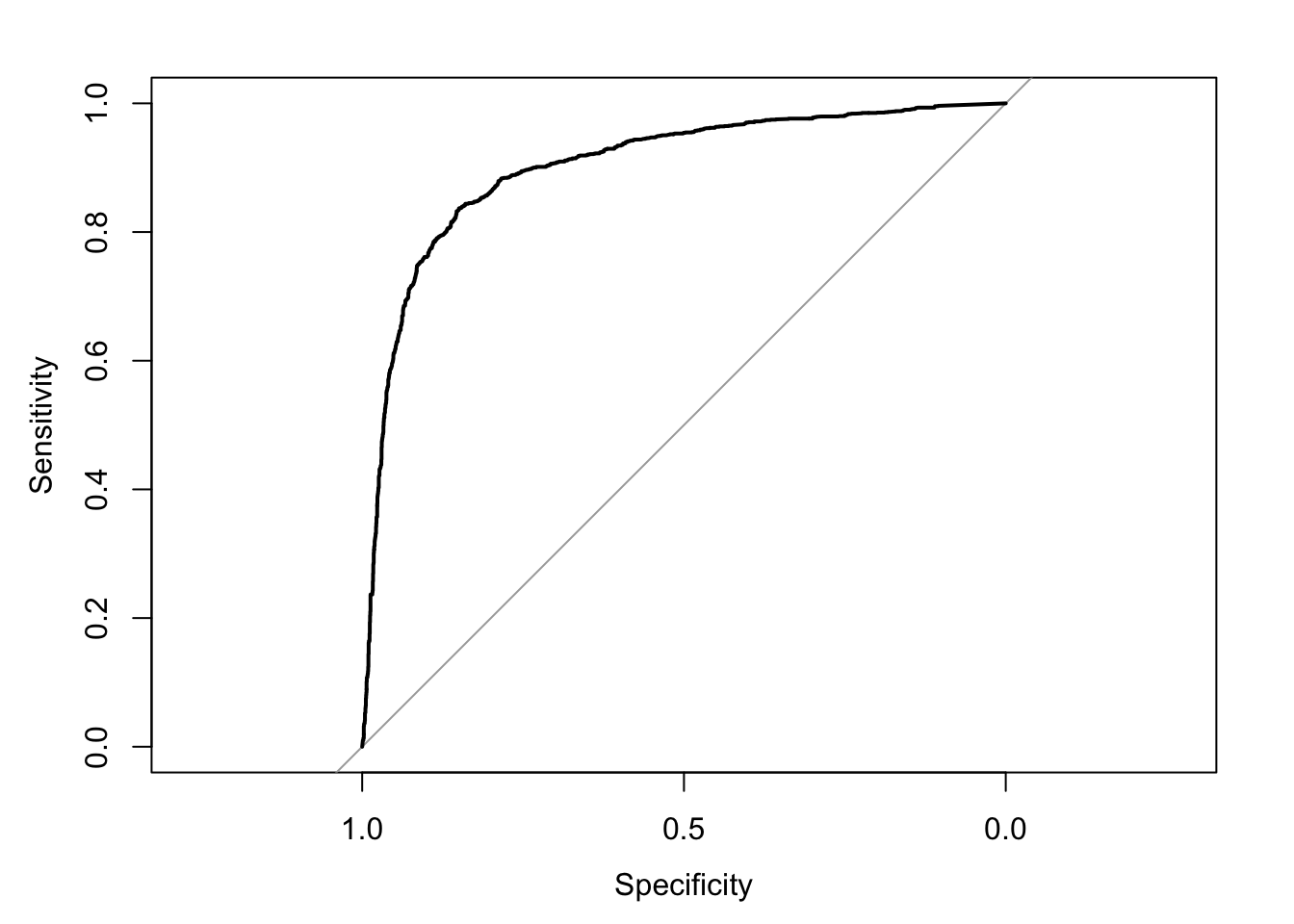

> roc2 <- roc(spam$spam, p2); plot(roc2)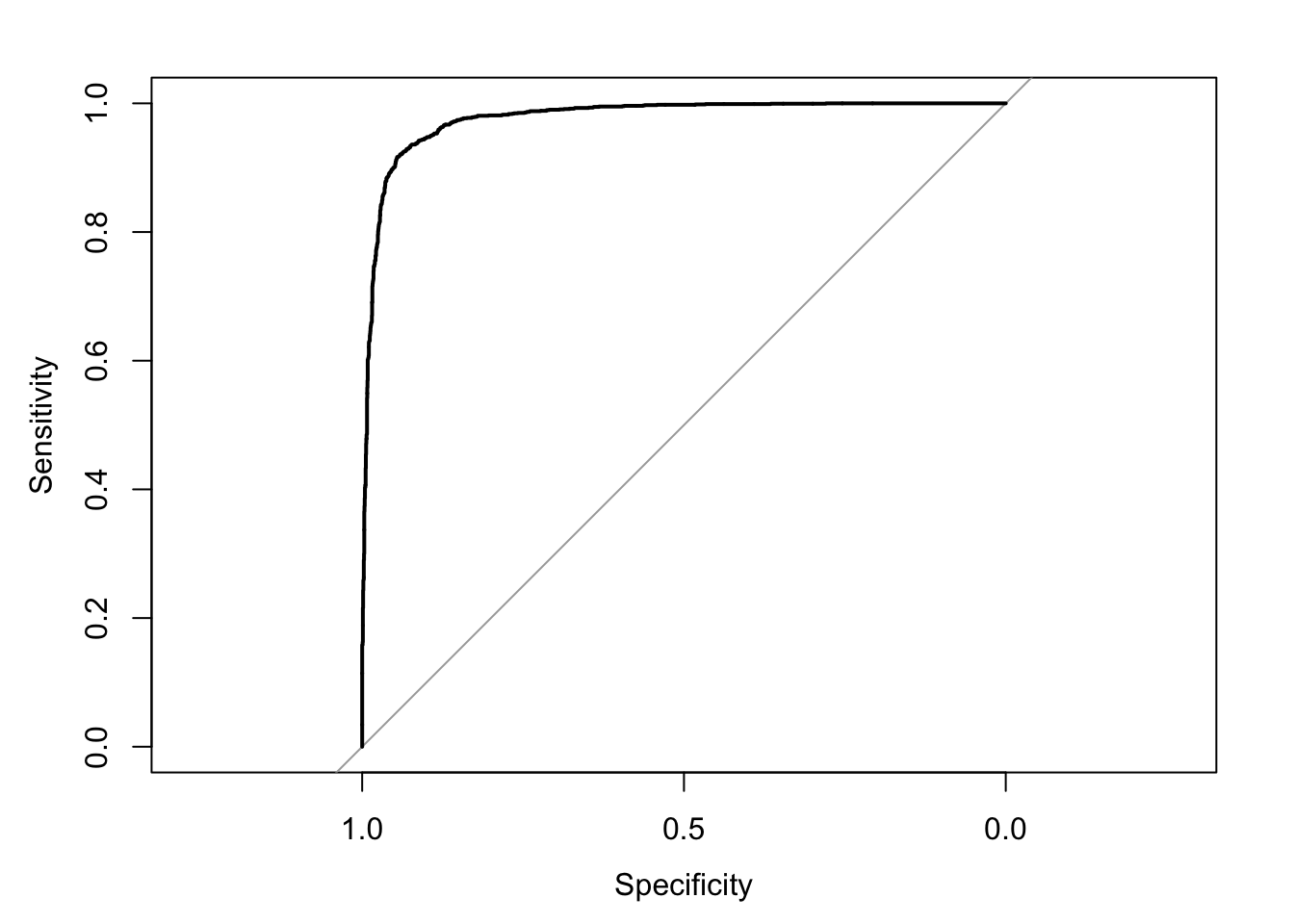

> auc1 <- auc(roc1); print(auc1)

#> Area under the curve: 0.9021

> auc2 <- auc(roc2); print(auc2)

#> Area under the curve: 0.9774

Con base en los resultados de (3) y (4), elige un modelo y define un umbral τ para clasificar correos como spam o no-spam.

El modelo mas complejo es más predictivo. Elegimos un umbral relativamente estricto: τ = 0.7

Con τ = 0.7 exigimos más “evidencia” antes de etiquetar un correo como spam.
Esto reduce falsos positivos (legítimos mal clasificados como spam), a costa de aumentar falsos negativos (spam que se cuelan).
Es razonable si nuestra prioridad es no perder correos legítimos.

> tau <- 0.7

Usando el modelo y umbral seleccionados en (5), construye una matriz de confusión. Elige una métrica relevante (accuracy, recall, precisión o F1), justifica tu elección e interpreta los resultados.

> pred_class <- ifelse(p2 > tau, 1, 0)
> 
> cm <- confusionMatrix(factor(pred_class),
+                       factor(spam$spam),
+                       positive = "1")
> print(cm)

#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction    0    1
#>          0 2711  319
#>          1   77 1494
#>                                           
#>                Accuracy : 0.9139          
#>                  95% CI : (0.9055, 0.9219)
#>     No Information Rate : 0.606           
#>     P-Value [Acc > NIR] : < 2.2e-16       
#>                                           
#>                   Kappa : 0.8155          
#>                                           
#>  Mcnemar's Test P-Value : < 2.2e-16       
#>                                           
#>             Sensitivity : 0.8240          
#>             Specificity : 0.9724          
#>          Pos Pred Value : 0.9510          
#>          Neg Pred Value : 0.8947          
#>              Prevalence : 0.3940          
#>          Detection Rate : 0.3247          
#>    Detection Prevalence : 0.3414          
#>       Balanced Accuracy : 0.8982          
#>                                           
#>        'Positive' Class : 1               
#>

El modelo clasifica correctamente el 91% de los correos (Accuracy). Del total de spam, el modelo detecta un 82% (Sensitivity/Recall). Del total de correos legítimos, el modelo reconoce correctamente un 97% (Specificity ≈ 97%).

Este modelo tiene buena performance pero prioriza minimizar falsos positivos (no molestar al usuario con mails legítimos marcados como spam), a costa de aceptar un cierto nivel de falsos negativos (spam que logra pasar).

Repite la comparación entre ambos modelos utilizando validación cruzada k-fold. Evalúa si el modelo que considerabas mejor se mantiene como preferido o si cambia la conclusión. En caso de que cambie, explica por qué ocurrió este cambio. Finalmente, reporta los resultados de la matriz de confusión promediada a partir de la validación cruzada.

> library(tidyverse)
> library(caret)
> library(pROC)
> 
> 
> set.seed(123)
> ctrl <- trainControl(
+   method = "cv",
+   number = 10,
+   summaryFunction = twoClassSummary,
+   classProbs = TRUE,
+   savePredictions = TRUE
+ )
> 
> spam$spam <- factor(ifelse(spam$spam == 1, "spam", "not_spam"))
> 
> 
> m1_cv <- train(
+   spam ~ word_freq_free + word_freq_money + char_freq_exc + capital_run_length_average,
+   data = spam,
+   method = "glm",
+   family = "binomial",
+   trControl = ctrl,
+   metric = "ROC"
+ )
> 
> m2_cv <- train(
+   spam ~ .,
+   data = spam,
+   method = "glm",
+   family = "binomial",
+   trControl = ctrl,
+   metric = "ROC"
+ )
> 
> res <- resamples(list(M1 = m1_cv, M2 = m2_cv))
> summary(res)

#> 
#> Call:
#> summary.resamples(object = res)
#> 
#> Models: M1, M2 
#> Number of resamples: 10

#> ROC 
#>         Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
#> M1 0.8762155 0.8966651 0.9034389 0.9021040 0.9089734 0.9172969    0
#> M2 0.9569630 0.9686340 0.9728439 0.9715653 0.9776604 0.9796234    0
#> 
#> Sens 
#>         Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
#> M1 0.9136691 0.9399642 0.9461399 0.9426020 0.9462366 0.9641577    0
#> M2 0.9172662 0.9433937 0.9516129 0.9504874 0.9614695 0.9749104    0
#> 
#> Spec 
#>         Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
#> M1 0.5745856 0.6217367 0.6346154 0.6326574 0.6629834 0.6740331    0
#> M2 0.8563536 0.8784530 0.8898215 0.8869316 0.8954602 0.9116022    0

> bwplot(res, main = "Comparación de desempeño por validación cruzada (10-fold)")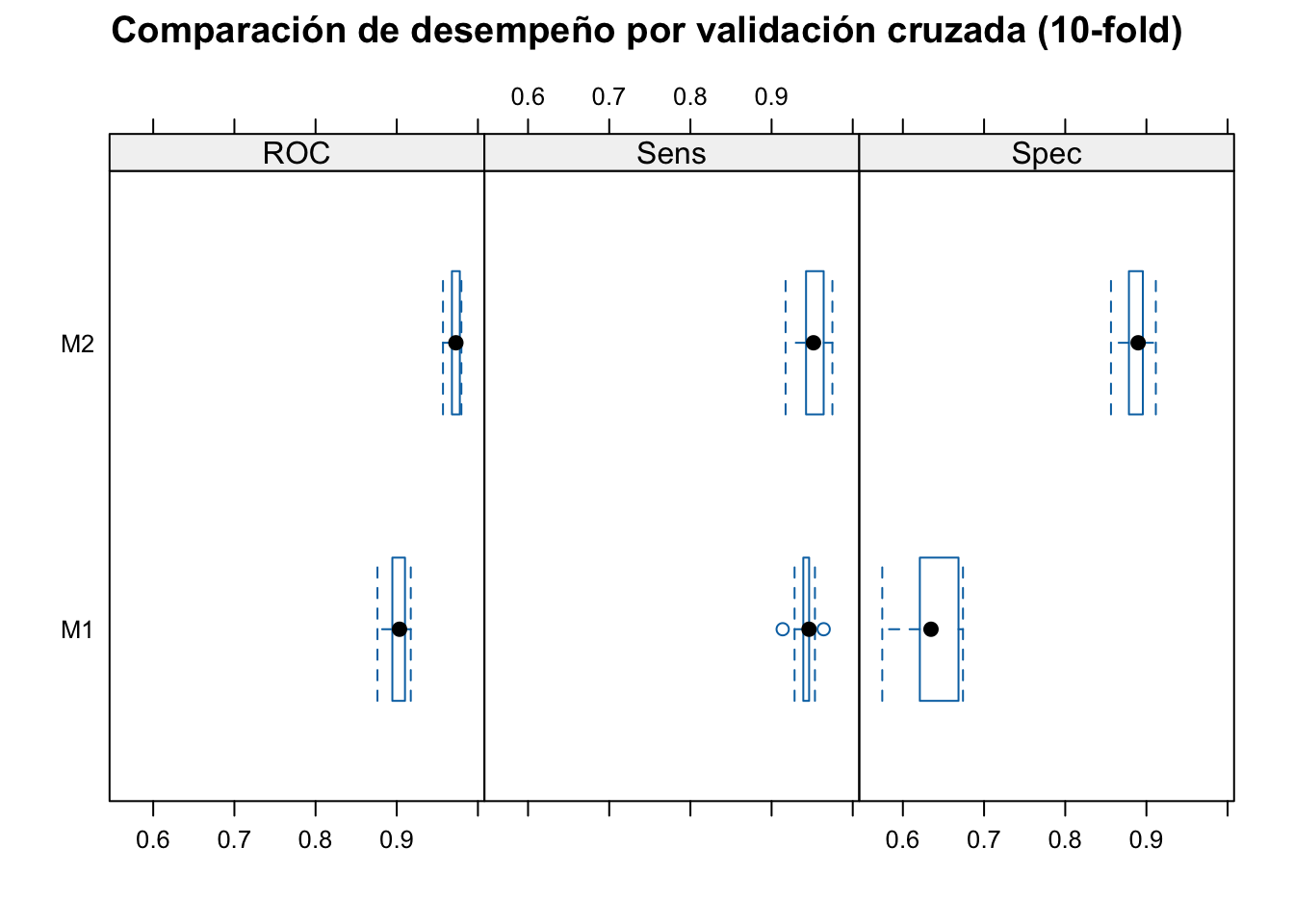

> dotplot(res)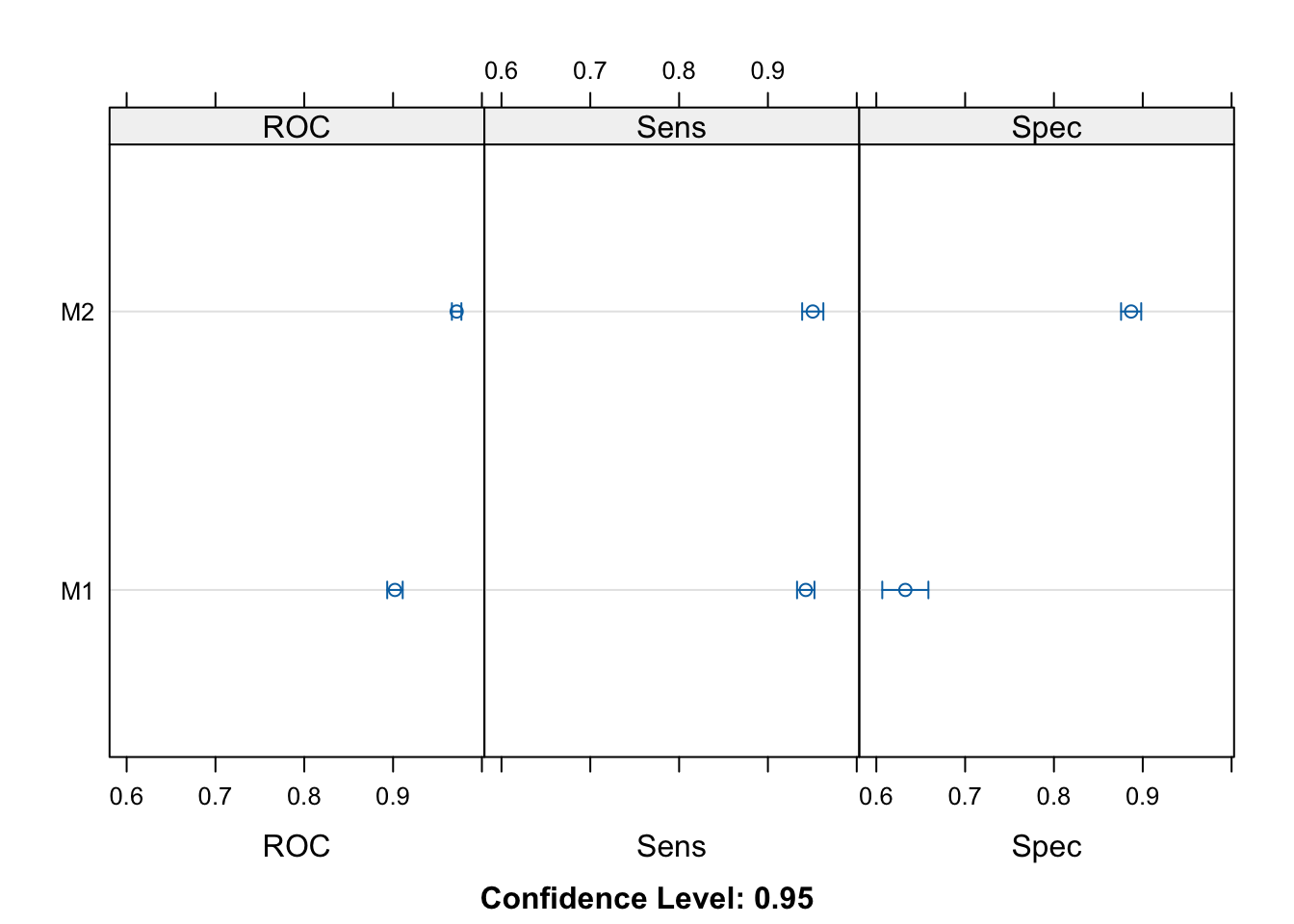

> # Obtener predicciones del modelo más predictivo
> mean(m1_cv$results$ROC); mean(m2_cv$results$ROC)

#> [1] 0.902104

#> [1] 0.9715653

Modelo con mejor AUC promedio es el más complejo.

> tau <- 0.7
> preds <- m2_cv$pred
> 
> # Clasificación con τ = 0.7
> preds$pred_tau <- ifelse(preds$spam > tau, "spam", "not_spam") |> factor(levels = c("not_spam", "spam"))
> 
> # Matriz de confusión promedio (promedio sobre folds)
> cm <- confusionMatrix(preds$pred_tau, preds$obs, positive = "spam")
> cm

#> Confusion Matrix and Statistics
#> 
#>           Reference
#> Prediction not_spam spam
#>   not_spam     2700  328
#>   spam           88 1485
#>                                           
#>                Accuracy : 0.9096          
#>                  95% CI : (0.9009, 0.9177)
#>     No Information Rate : 0.606           
#>     P-Value [Acc > NIR] : < 2.2e-16       
#>                                           
#>                   Kappa : 0.8062          
#>                                           
#>  Mcnemar's Test P-Value : < 2.2e-16       
#>                                           
#>             Sensitivity : 0.8191          
#>             Specificity : 0.9684          
#>          Pos Pred Value : 0.9441          
#>          Neg Pred Value : 0.8917          
#>              Prevalence : 0.3940          
#>          Detection Rate : 0.3228          
#>    Detection Prevalence : 0.3419          
#>       Balanced Accuracy : 0.8938          
#>                                           
#>        'Positive' Class : spam            
#>

El modelo completo mantiene un mejor desempeño promedio en validación cruzada, con mayor AUC, confirmando que su complejidad se traduce en mejor capacidad predictiva y generalización. La matriz de confusión promedio muestra alta sensibilidad y especificidad, indicando que el modelo generaliza bien sin sobreajustar excesivamente.