SOC3070 Análisis de Datos Categóricos

Author

Tarea corta 3

> # Instalar y cargar paquetes necesarios
> # install.packages("titanic")
> library(tidyverse)
> library(titanic)
> 
> # cargar datos
> data("titanic_train")
> df <- titanic_train %>%
+   filter(Pclass == 3, !is.na(Age)) %>%
+   mutate(Sex = factor(Sex),
+          Survived = as.numeric(Survived))

Ponderación: 6% de la nota final del curso.

\(\newcommand{\vect}[1]{\boldsymbol{#1}}\)

Datos:

En esta tarea usaremos el dataset titanic_train incluido en el paquete titanic. El conjunto contiene información sobre pasajeros del Titanic: clase económica, edad, sexo y si sobrevivieron (Survived = 1) o no (Survived = 0).

Nos restringiremos a los pasajeros de clase 3 (Pclass==3).

> df %>% glimpse()

#> Rows: 355
#> Columns: 12
#> $ PassengerId <int> 1, 3, 5, 8, 9, 11, 13, 14, 15, 17, 19, 23, 25, 26, 38, 39,…
#> $ Survived    <dbl> 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0…
#> $ Pclass      <int> 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3…
#> $ Name        <chr> "Braund, Mr. Owen Harris", "Heikkinen, Miss. Laina", "Alle…
#> $ Sex         <fct> male, female, male, male, female, female, male, male, fema…
#> $ Age         <dbl> 22.0, 26.0, 35.0, 2.0, 27.0, 4.0, 20.0, 39.0, 14.0, 2.0, 3…
#> $ SibSp       <int> 1, 0, 0, 3, 0, 1, 0, 1, 0, 4, 1, 0, 3, 1, 0, 2, 1, 1, 0, 1…
#> $ Parch       <int> 0, 0, 0, 1, 2, 1, 0, 5, 0, 1, 0, 0, 1, 5, 0, 0, 0, 0, 0, 0…
#> $ Ticket      <chr> "A/5 21171", "STON/O2. 3101282", "373450", "349909", "3477…
#> $ Fare        <dbl> 7.2500, 7.9250, 8.0500, 21.0750, 11.1333, 16.7000, 8.0500,…
#> $ Cabin       <chr> "", "", "", "", "", "G6", "", "", "", "", "", "", "", "", …
#> $ Embarked    <chr> "S", "S", "S", "S", "S", "S", "S", "S", "S", "Q", "S", "Q"…

Problema:

En particular, estimaremos un modelo de regresión logística para predecir la probabilidad de sobrevivir en función de la edad y el sexo, permitiendo un efecto no lineal de la edad:

\[ \text{logit}(P(\text{Survived}=1)) = \beta_0 + \beta_1 \cdot \text{Age} + \beta_2 \cdot \text{Age}^2 + \beta_3 \cdot \text{Sex} + \beta_4 \cdot (\text{Age} \times \text{Sex}) \]

En R:

> modelo_titanic <- glm(Survived ~ Age + I(Age^2) + Sex + Age:Sex,
+                       data=df, family=binomial)
> summary(modelo_titanic)

#> 
#> Call:
#> glm(formula = Survived ~ Age + I(Age^2) + Sex + Age:Sex, family = binomial, 
#>     data = df)
#> 
#> Coefficients:
#>               Estimate Std. Error z value Pr(>|z|)  
#> (Intercept)  0.5437824  0.4760911   1.142   0.2534  
#> Age         -0.0380258  0.0336973  -1.128   0.2591  
#> I(Age^2)     0.0001913  0.0006222   0.307   0.7585  
#> Sexmale     -1.2554611  0.5763530  -2.178   0.0294 *
#> Age:Sexmale -0.0090570  0.0228499  -0.396   0.6918  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 390.81  on 354  degrees of freedom
#> Residual deviance: 345.68  on 350  degrees of freedom
#> AIC: 355.68
#> 
#> Number of Fisher Scoring iterations: 5

1. Probabilidades estimadas

Calcula y grafica la probabilidad de sobrevivencia estimada por el modelo para hombres y mujeres en todo el rango de edad. El resultado debe verse así:

> ages <- seq(min(df$Age), max(df$Age), 1)
> newdata <- expand.grid(Age=ages, Sex=levels(df$Sex))
> newdata$pred <- predict(modelo_titanic, newdata, type="response")
> 
> ggplot(newdata, aes(x=Age, y=pred, color=Sex)) +
+   geom_line(size=1.2) +
+   labs(title="Probabilidad de sobrevivencia",
+        x="Edad", y="Probabilidad de sobrevivencia") +
+   scale_color_julia() +
+   theme_julia()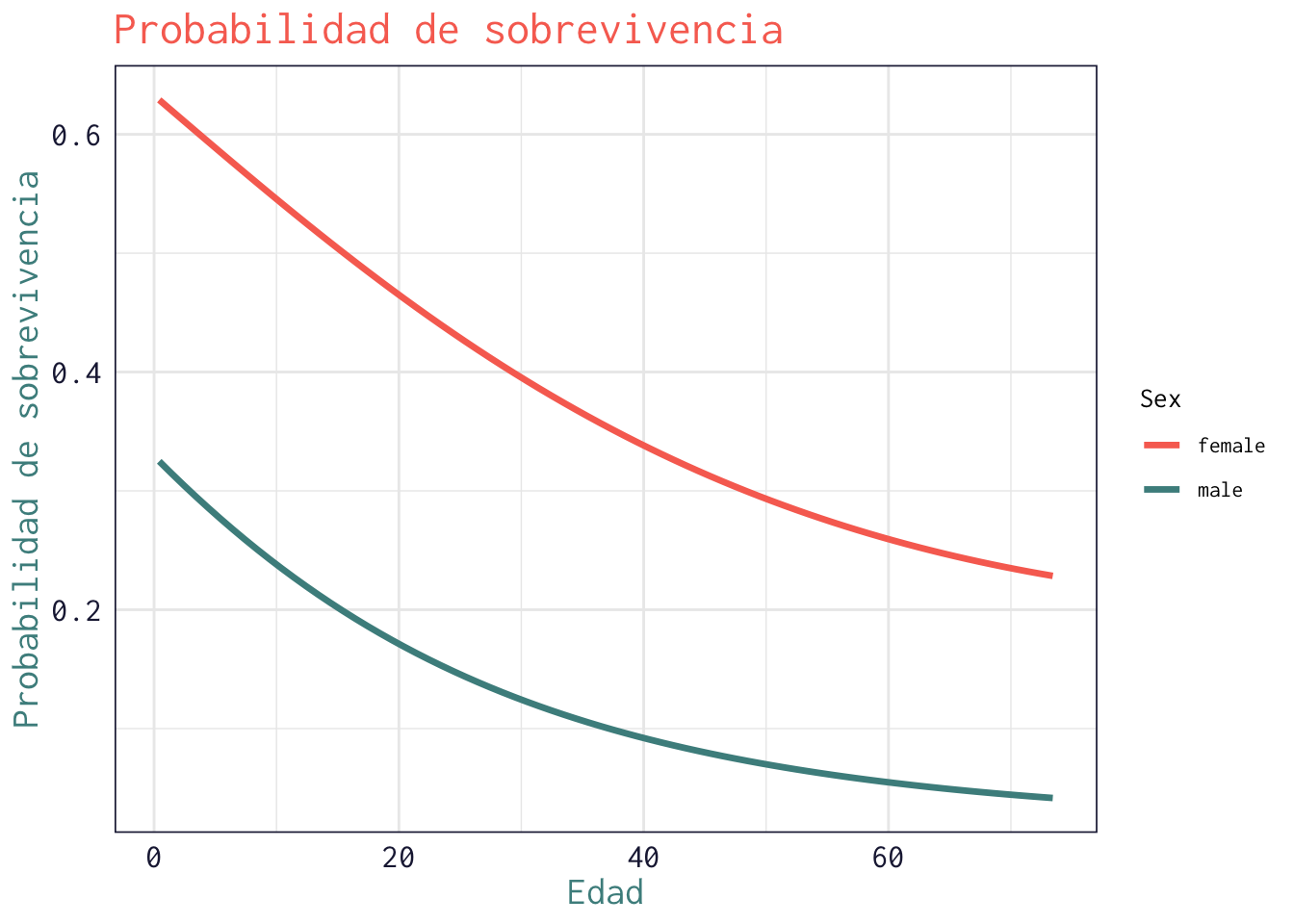

2. Diferencia hombres − mujeres

Calcula la diferencia en probabilidades de sobrevivencia entre hombres y mujeres (hombres − mujeres) para cada edad.

> obs <- newdata %>%
+   pivot_wider(names_from=Sex, values_from=pred) %>%
+   mutate(diff = male - female)
> head(obs)

#> # A tibble: 6 × 4
#>     Age female  male   diff
#>   <dbl>  <dbl> <dbl>  <dbl>
#> 1  0.42  0.629 0.325 -0.304
#> 2  1.42  0.620 0.315 -0.305
#> 3  2.42  0.611 0.305 -0.307
#> 4  3.42  0.603 0.295 -0.307
#> 5  4.42  0.594 0.286 -0.308
#> 6  5.42  0.585 0.277 -0.308

3. Bootstrap para intervalos de confianza

Usa bootstrap (500 réplicas) para estimar un intervalo de confianza al 95% para la diferencia en probabilidades entre hombres y mujeres en cada edad. Grafica la curva estimada junto con su intervalo. El resultado debe verse similar a esto:

> set.seed(123)
> 
> boot_fun <- function(data){
+   m <- glm(Survived ~ Age + I(Age^2) + Sex + Age:Sex,
+            data=data, family=binomial)
+   nd <- expand.grid(Age=ages, Sex=levels(data$Sex))
+   nd$pred <- predict(m, nd, type="response")
+   nd %>%
+     pivot_wider(names_from=Sex, values_from=pred) %>%
+     mutate(diff = male - female) %>%
+     pull(diff)
+ }
> 
> B <- 500
> boot_diffs <- replicate(B, boot_fun(df[sample(nrow(df), replace=TRUE), ]))
> 
> ci <- apply(boot_diffs, 1, quantile, c(0.025, 0.975), na.rm=TRUE)
> ci_df <- obs %>%
+   mutate(lower = ci[1,], upper = ci[2,])
> 
> ggplot(ci_df, aes(x=Age, y=diff)) +
+   geom_line(aes(color="diff"), size=1) +
+   geom_ribbon(aes(ymin=lower, ymax=upper, fill="IC 95%"), alpha=0.2) +
+   geom_hline(yintercept=0, linetype="dashed", color=julia$navy) +
+   labs(title="Diferencia en probabilidad de sobrevivencia",
+        x="Edad", y="Diferencia de probabilidades",
+        color="", fill="") +
+   scale_color_julia() +
+   scale_fill_julia() +
+   theme_julia()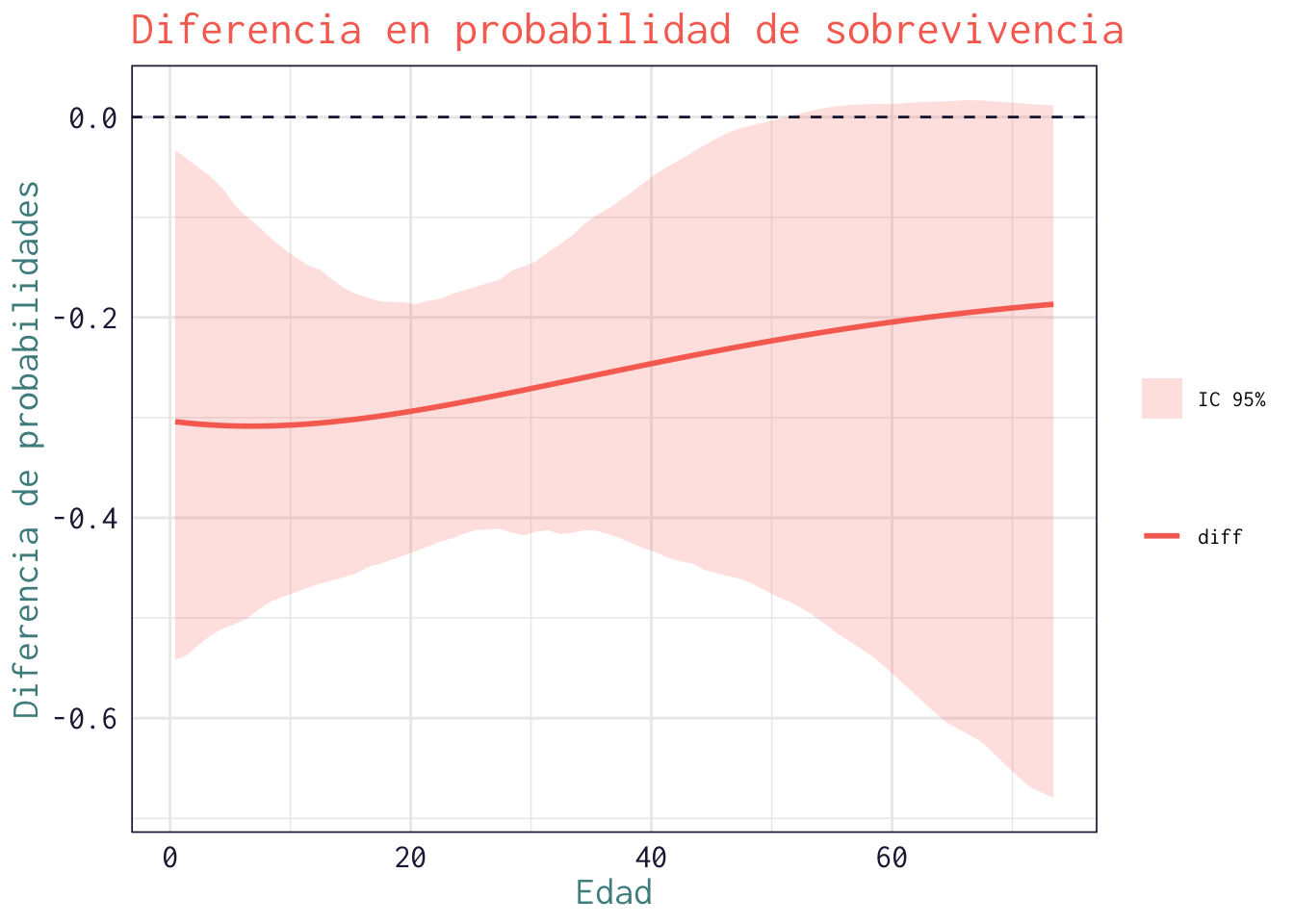

Si la curva está por encima de 0, los hombres de esa edad tienen mayor probabilidad de sobrevivir que las mujeres. Si está por debajo de 0, ocurre lo contrario. La banda sombreada muestra la incertidumbre (IC 95%) alrededor de la diferencia.