class: center, middle, inverse, title-slide .title[ # Probabilidad e Inferencia Estadística ] .subtitle[ ## Teoremas Asintóticos ] .author[ ### <br> Mauricio Bucca <br> <a href="https://github.com/mebucca">github.com/mebucca</a> <br> <a href="mailto:mebucca@uc.cl" class="email">mebucca@uc.cl</a> ] .date[ ### 23 September, 2025 ] --- class: inverse, center, middle #Teoremas Asintóticos --- class: inverse, center, middle #Ley de los Grandes Números ## Convergencia en Probabilidad --- ## Ley de los Grandes Números - `\(X\)` es una variable aleatoria con primer momento `\(\mathbb{E}(X) = \mu\)` - Generamos/tomamos una muestra `\(\{X_{1},X_{2}, \dots, X_{n}\}\)` de tamaño `\(n\)` donde: - Cada `\(X_{i}\)` sigue la misma distribución que la variable aleatoria `\(X\)` - Las `\(X_{i}\)`'s son independientes entre si -- - La media aritmética en .bold[esta muestra] es `\(\bar{X}_{n} = \frac{1}{n}\sum_{i=1}^{n}X_i\)` - `\(\bar{X}_{n}\)` es .bold[aleatoria] porque las `\(X_{i}\)`'s son aleatorias. <br> -- .bold[Ley de los Grandes Números] establece que, a medida que el tamaño de una muestra aleatoria crece, la media aritmética de la muestra .bold[converge en probabilidad] al promedio teórico/poblacional: `\(\bar{X} \overset{p}{\to} \mathbb{E}(X)\)`. .content-box-primary[ .bolder[Matemáticamente,] `$$\color{white}{\lim_{n \to \infty}\mathbb{P}\left( \left| \bar{X} - \mu \right| \geq \epsilon \right) = 0}$$` ] --- ## Ley de los Grandes Números .bold[Convergencia en Probabilidad] .pull-left[ 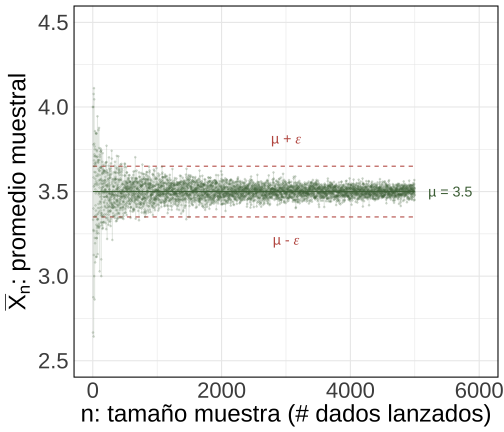<!-- --> ] .pull-right[ 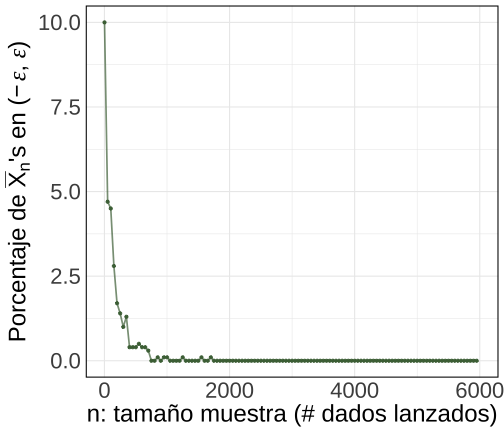<!-- --> ] --- class: inverse, center, middle #Valor Esperado y Varianza #de la #Media Muestral --- ##Valor Esperado de la Media Muestral .pull-left[ - `\(X\)` es una variable aleatoria con primer momento `\(\mathbb{E}(X) = \mu\)` - Generamos/tomamos una muestra `\(n\)` del tipo: - `\(\{X_{1},X_{2}, \dots, X_{n}\}\)` - Las `\(X_{i}\)`'s son .bold[iid] - En cada muestra calculamos la .bold[media muestral], `\(\bar{X}_{n}\)` - `\(\bar{X}_{n}\)` es .bold[aleatoria] porque las `\(X_{i}\)`'s son aleatorias. <br> .bold[¿Cuál es el promedio de dichas medias muestrales?] ] -- .pull-right[ `\begin{align} \mathbb{E}(\bar{X}_{n}) &= \mathbb{E}\big(\frac{1}{n} \sum^{n}_{i=1} X_{i} \big) \\ \\ &=\frac{1}{n}\mathbb{E}\big( X_{1} + X_{2} + \cdots + X_{n} \big) \\ \\ &=\frac{1}{n}\big( \mathbb{E}(X_{1}) + \mathbb{E}(X_{2}) + \cdots + \mathbb{E}(X_{n})\big) \\ \\ &=\frac{1}{n}\big( \mu + \mu + \cdots + \mu \big) \\ \\ &=\frac{1}{n}\big( n \mu \big) \\ \\ &=\mu \end{align}` ] --- ##Valor Esperado de la Media Muestral Para cualquier `\(n\)` el promedio de esas las diferentes `\(\bar{X}_{n}\)`'s es igual a `\(\mathbb{E}(X)\)`. .center[ 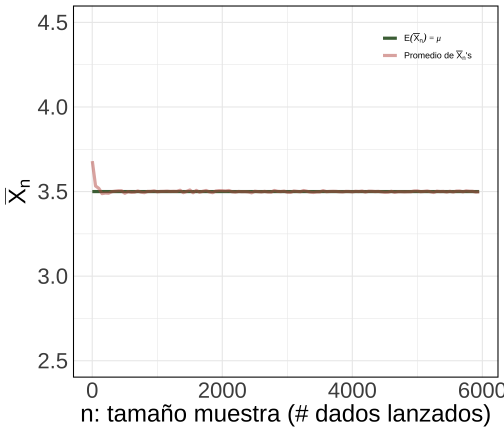<!-- --> ] --- ## Varianza y Desviación Standard de la Media Muestral .pull-left[ - `\(X\)` es una variable aleatoria con primer momento `\(\mathbb{E}(X) = \mu\)` - Generamos/tomamos una muestra `\(n\)` del tipo: - `\(\{X_{1},X_{2}, \dots, X_{n}\}\)` - Las `\(X_{i}\)`'s son .bold[iid] - En cada muestra calculamos la .bold[media muestral], `\(\bar{X}_{n}\)` - `\(\bar{X}_{n}\)` es .bold[aleatoria] porque las `\(X_{i}\)`'s son aleatorias. <br> .bold[¿Cuanto varían dichas medias muestrales?] ] -- .pull-right[ `\begin{align} \text{Var}(\bar{X}) &= \text{Var}\big(\frac{1}{n} \sum^{n}_{i=1} X_{i} \big) \\ &= \frac{1}{n^2} \text{Var}\big( \sum^{n}_{i=1} X_{i} \big) \\ \\ &=\frac{1}{n^2}\big( \text{Var}(X_{1}) + \text{Var}(X_{2}) + \cdots + \text{Var}(X_{n})\big) \\ \\ &=\frac{1}{n^2}\big( \sigma^2 + \sigma^2 + \cdots + \sigma^2 \big) \\ \\ &=\frac{1}{n^2}\big( n \sigma^2 \big) \\ \\ &=\frac{\sigma^2}{n} \implies \quad \sqrt{\text{Var}(\bar{X})} = \frac{\sigma}{\sqrt{n}} \end{align}` ] --- ## Varianza de la Media Muestral A medida que aumenta `\(n\)` los diferentes `\(\bar{X}_{n}\)`'s se concentran más cerca del promedio de las `\(\bar{X}_{n}\)`'s (que, a su vez, coincide con `\(\mathbb{E}(X)\)`). .center[ 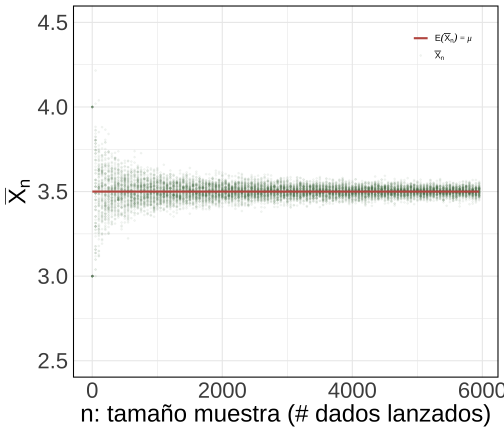<!-- --> ] --- ## Varianza de la Media Muestral A medida que aumenta `\(n\)` la desviación standard de `\(\bar{X}_{n}\)`'s .bold[disminuye a una taza decreciente] específica. .center[ <!-- --> ] --- ## Corolario Típicamente contamos con .bold[sólo una muestra], con un `\(n\)` fijo. .bold[¿"Cuán bien" nuestro estimado muestral] `\(\bar{X}_{n}\)` .bold[captura el parámetro verdadero E(X)?] -- .center[ <!-- --> ] --- class: inverse, center, middle ##Hasta la próxima clase. Gracias! <br> Mauricio Bucca <br> https://mebucca.github.io/ <br> github.com/mebucca