Probabilidad e Inferencia Estadística

class: center, middle, inverse, title-slide

.title[
# Probabilidad e Inferencia Estadística
]
.subtitle[
## #4: Variables Aleatorias Discretas
]
.author[
### Mauricio Bucca <a href="https://github.com/mebucca">github.com/mebucca</a> <a href="mailto:mebucca@uc.cl" class="email">mebucca@uc.cl</a>
]

---

class: inverse, center, middle

---
class: inverse, center, middle

##Distribuciones Discretas
### Intuición

---
### Tiro de penal

Final de la Copa Mundial de la FIFA 1994. Roberto Baggio va a tirar su penal ...

.pull-left[

.bold[Número finito de resultados posibles]:

- Gol
- Fallo

.bold[Evento aleatorio]:

- Existe una probabilidad asociada a cada resultado

]

.pull-right[
 
 
 
.center[![baggio](baggio.gif)]
]

---
class: inverse, center, middle

## Distribuciones Discretas
### Distribución Bernoulli

---

### Distribución Bernoulli

.pull-left[
- Experimento: tiramos una moneda al aire.

- `$X$` es una variable aleatoria tal que `$X=1$` (Cara) o `$X=0$` (Sello).

- La probabilidad de obtener Cara es `$p=0.7$` y la de Sello es `$1-p = 0.3$`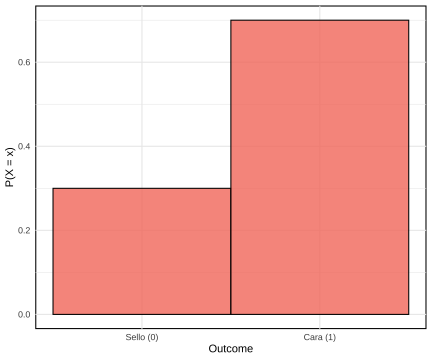

![](class_4_files/figure-html/unnamed-chunk-1-1.png)

]

.pull-right[

.bold[Función de masa probabilistica (PMF):]

X es una variable aleatoria Bernoulli, es decir

`\begin{align}
f(x) =
  \begin{cases}
    p  & \quad \text{si } x=1\\
    1 - p  & \quad \text{si } x=0 \\
    0 & \quad \text{otro}
  \end{cases}
\end{align}`

En modo más sintético:

`$$f(x) = p^{x}(1-p)^{1-x}  \quad \text{si } x=1 \text{ o } x=0$$`

]

---

### Distribución Bernoulli

.bold[Ilustración via simulación en] `R`

Tiremos una moneda con probabilidad de obtener "Cara" ( `$1$` ) de 70% ( `$p=0.7$` )

``` r
#set.seed(12347)
moneda <- rbinom(n=1, size=1, p=0.7)
```

```
## Warning in rbinom(n = 1, size = 1, p = 0.7): partial argument match of 'p' to
## 'prob'
```

``` r
print(moneda)
```

```
## [1] 1
```

--

Repitamos el proceso 1000 veces ...

``` r
#set.seed(12347)
monedas <- rbinom(n=1000, size=1, p=0.7)
```

```
## Warning in rbinom(n = 1000, size = 1, p = 0.7): partial argument match of 'p'
## to 'prob'
```

```
##  [1] 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 1 1 1
```

```
## [1] "P(Cara) =  0.702"
```

---
class: inverse, center, middle

## Distribuciones Discretas
### Distribución Binomial

---

### Distribución Binomial

La distribución binomial es la distribución de la suma de variables Bernoulli *independientes y con distribución idéntica* (.bold[iid]).

--

Ejemplo,

- Supongamos que `$X$` es una variable de Bernoulli que toma el valor 1 cuando se obtiene "Cara" al lanzar una moneda

- `$\mathbb{P}(X=1)=p$`

--

- Ahora, supongamos que lanzamos la misma moneda 3 veces. Llamamos a estas variables `$X_{1}, X_{2}, X_{3}$`

- Definamos `$Y = X_{1} + X_{2} + X_{3}$`

- `$Y$` sigue una distribución Binomial, o `$Y \sim \text{Binomial}$`

---
### Distribución Binomial

.bold[Ejercicio rápido:]

.content-box-primary[
.bolder[Pregunta 1:]
¿Cuál es la probabilidad de obtener tres "Caras"? Es decir, ¿Cuál es la probabilidad de que `$Y=3$`?]

.content-box-secondary[
- Dado que los 3 ensayos son independientes podemos expresar esta probabilidad como:

`$$\mathbb{P}(Y=3) = \mathbb{P}(X_{1}=1,X_{2}=1,X_{3}=1) = \mathbb{P}(X_{1}=1)\mathbb{P}(X_{2}=1)\mathbb{P}(X_{3}=1)$$`

- Y dado que las tres variables distribuyen Bernoulli con la misma probabilidad `$p$`, obtenemos:

`$$\mathbb{P}(Y=3) = p \times p \times p =  p^{3}$$`
]
---
### Distribución Binomial

.content-box-primary[
.bolder[Pregunta 2:]
¿Cuál es la probabilidad de obtener 2 "Caras" con 3 tiros? Es decir, ¿Cuál es la probabilidad de que `$Y=2$`?
]

- Por simpleza, consideremos la siguiente secuencia: `$\{X_{1}=1,X_{2}=1,X_{3}=0\}$`, que satisface `$Y=2$`

- La probabilidad de obtener esta secuencia es:

`\begin{align}
  \mathbb{P}(X_{1}=1,X_{2}=1,X_{3}=0)  &= \mathbb{P}(X_{1}=1) \times \mathbb{P}(X_{2}=1) \times \mathbb{P}(X_{3}=0)  \\
                              &= p \times p \times (1-p) =  p^{2}(1-p)
\end{align}`

- Sin embargo, hay 3 secuencias que satisfacen `$Y=2$`.
--
 También `$\{X_{1}=1,X_{2}=0,X_{3}=1\}$` y `$\{X_{1}=0,X_{2}=1,X_{3}=1\}$`, cada una con probabilidad de ocurrencia `$p^{2}(1-p)^{1}$`. Por tanto:

.content-box-secondary[
.bolder[Respuesta:] la probabilidad de conseguir 2 "Caras" con 3 tiros es:
`$$\mathbb{P}(Y=2) = 3 \times  p^{2}(1-p)^{1}$$`
]

---

### Distribución Binomial

.bold[Generalización]: lanzamos la misma moneda `$n$` veces y la variable `$Y$` cuantifica el número de "Caras" (1) obtenidas.

`$$Y = \sum^{n}_{i=1} X_{i}$$`
--

.content-box-primary[
.bolder[Pregunta:]
¿Cuál es la probabilidad de conseguir `$y$` "Caras" con `$n$` tiros?
]

* La probabilidad de obtener una secuencia particular con `$y$` "Caras" a partir de `$n$` lanzamientos es `$p^{y}(1-p)^{n-y}$`

* Existen `${n \choose y} = \frac{n!}{y! (n-y)!}$` secuencias de este tipo...

--
Por tanto,

`$$\mathbb{P}(Y=y) = f(y) = \frac{n!}{y! (n-y)!} \times p^{y} (1-p)^{n-y}$$`
--
En otras palabras, `$Y$` distribuye binomial con .bold[parámetros] `$n$` y `$p$`: `$Y \sim \text{Binomial}(n,p)$`

---
### Distribución Binomial

En práctica ...

- **Contexto**: Tenemos una moneda que, cuando se lanza, tiene una probabilidad de `$p = 0.6$` de caer en "Cara" y una probabilidad de `$1-p = 0.4$` de caer en "Sello".

- **Problema**:¿Cuál es la probabilidad de obtener 3 "Caras" con 10 lanzamientos?

- **Solución**: `$X \sim \text{Binomial}(n=10,p=0.6)$`

--

`$\quad \quad \quad \mathbb{P}(X=3) = \binom{10}{3} \times (0.6)^3 \times (0.4)^{10-3}$`

--

`$\quad \quad \quad \mathbb{P}(X=3) = \frac{10!}{3! \times 7!} \times (0.6)^3 \times (0.4)^7$`

--

`$\quad \quad \quad \mathbb{P}(X=3) = \frac{10 \times 9 \times \dots 1}{(3 \times 2 \times1) \times (7 \times 6 \times \dots 1 )} \times (0.6)^3 \times (0.4)^7$`

--

`$\quad \quad \quad \mathbb{P}(X=3) = 120 \times 0.216 \times 0.0028$`

--

`$\quad \quad \quad \mathbb{P}(X=3) \approx 0.0425$`

---

### f(x), Distribución Binomial

.pull-left[
- Ahora observamos la distribución completa

- La probabilidad de obtener `$0, 1, \dots, 10$` caras es: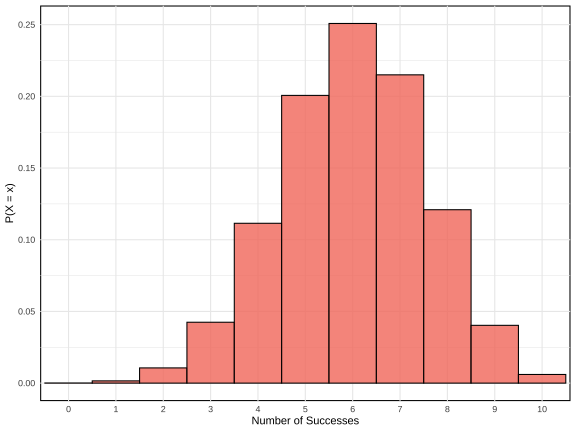

![](class_4_files/figure-html/unnamed-chunk-5-1.png)

]

.pull-right[

.bold[Función de masa probabilistica (PMF):]

X es una variable aleatoria Binomial, es decir

`\begin{align}
\mathbb{P}(X=x) = f(x) = \frac{n!}{x! (n-x)!}  p^{x} (1-p)^{n-x}
\end{align}`

En este caso,

`$n=10$` y `$p=0.6$`

]

---
### F(x), Distribución Binomial

.pull-left[
- Ahora observamos la distribución completa

- ¿Cual es la probabilidad de obtener 5 monedas o menos?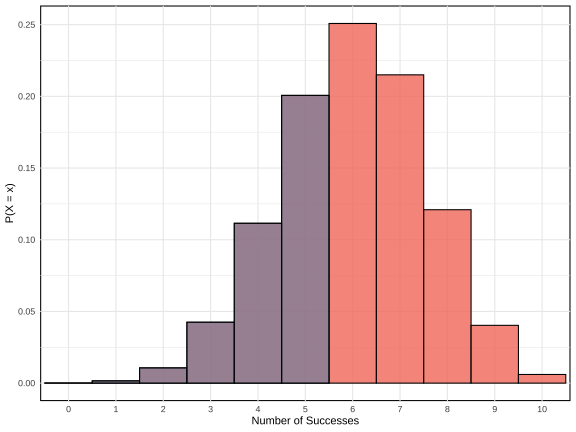

![](class_4_files/figure-html/unnamed-chunk-6-1.png)

]

.pull-right[

.bold[Función de distribución acumulada (CDF):]

X es una variable aleatoria Binomial, es decir

`\begin{align}
F(k; n, p) &= \mathbb{P}(X \leq k) \\ \\
           &= \sum_{i=0}^{k} \mathbb{P}(X=i) \\ \\
           &= \sum_{i=0}^{k} \frac{n!}{i! (n-i)!}  p^i (1-p)^{n-i} 
\end{align}`

En este caso,

`\begin{align}
F(k=5; n=10, p=0.6) &=  \mathbb{P}(X=0) + \dots + \mathbb{P}(X=5) \\ \\
                    &\approx 0.366
\end{align}`

]

---
### F(x), Distribución Binomial

.pull-left[
- Ahora observamos la distribución completa

- ¿Cual es la probabilidad de obtener 5 monedas o menos?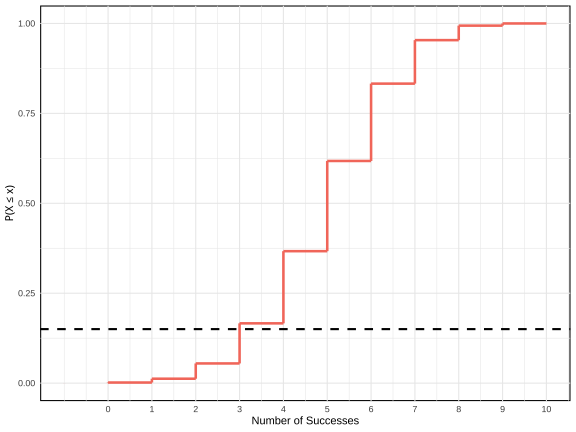

![](class_4_files/figure-html/unnamed-chunk-7-1.png)

]

.pull-right[

.bold[Función de distribución acumulada (CDF):]

X es una variable aleatoria Binomial, es decir

`\begin{align}
F(k; n, p) &= \mathbb{P}(X \leq k) \\ \\
           &= \sum_{i=0}^{k} \mathbb{P}(X=i) \\ \\
           &= \sum_{i=0}^{k} \frac{n!}{i! (n-i)!}  p^i (1-p)^{n-i} 
\end{align}`

En este caso,

`\begin{align}
F(k=5; n=10, p=0.6) &=  \mathbb{P}(X=0) + \dots + \mathbb{P}(X=5) \\ \\
                    &\approx 0.366
\end{align}`

]

---
class: inverse, center, middle

.huge[
**Hasta la próxima clase. Gracias!**
]

Mauricio Bucca 
https://mebucca.github.io/ 
github.com/mebucca