class: center, middle, inverse, title-slide .title[ # Probabilidad e Inferencia Estadística ] .subtitle[ ## Estimador y su Distribución Muestral ] .author[ ### <br> Mauricio Bucca <br> <a href="https://github.com/mebucca">github.com/mebucca</a> <br> <a href="mailto:mebucca@uc.cl" class="email">mebucca@uc.cl</a> ] .date[ ### 23 September, 2025 ] --- ## Estadística .center[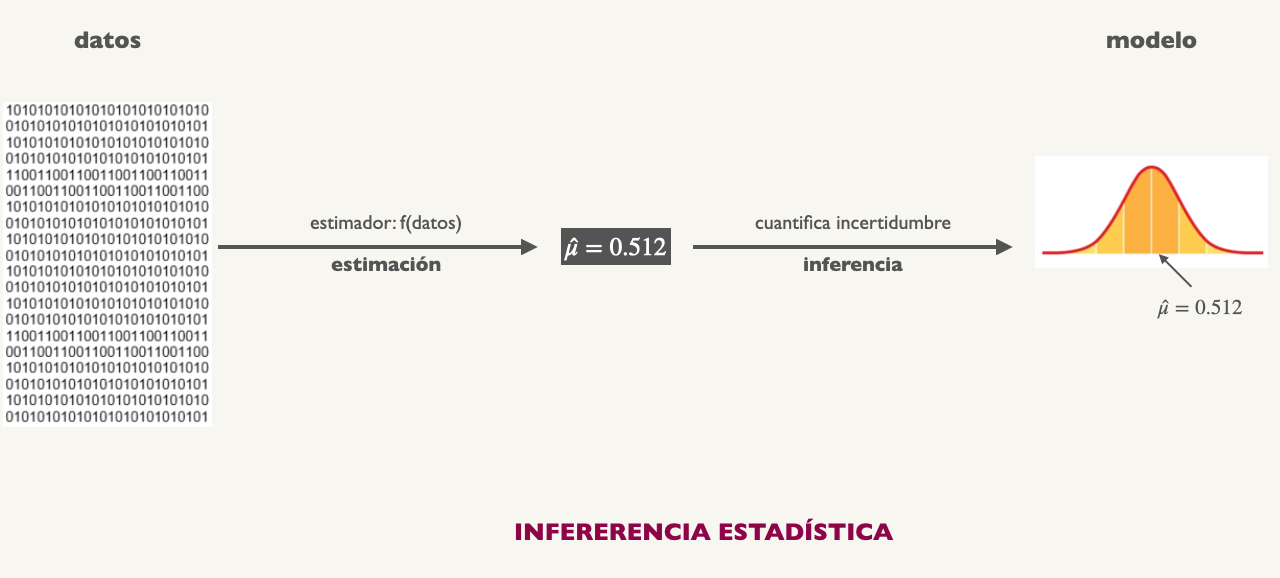] --- class: inverse, center, middle #Estimación --- #Estimación - Una socióloga quiere saber el promedio de años de escolaridad en USA -- - La socióloga toma una muestra aleatoria de 100 personas `\(m: \{X_1, \dots, X_{100} \}\)`. Los datos se ven así: -- .pull-left[ ``` ## # A tibble: 100 × 3 ## year educ age ## <fct> <dbl> <dbl> ## 1 1978 12 50 ## 2 2016 13 36 ## 3 2006 20 72 ## 4 1982 9 53 ## 5 2004 16 43 ## 6 1978 16 30 ## 7 1984 15 72 ## 8 2014 16 50 ## 9 1982 16 24 ## 10 1984 12 52 ## # ℹ 90 more rows ``` ] -- .pull-right[ <br> - .bold[Datos]: realización de `\(n\)` variables aleatorias - Normalmente *.bold[no conocemos]* la distribución de las variables. - .bold[Estadística]: aprender de los datos para .bold[estimar] los parámetros que los generan ] --- ## Estimando, Estimador y Estimado -- - El .bold[estimando] es aquello que queremos conocer. Dicho de otra forma, es el parámetro (poblacional/teórico) de interés. Llamémoslo `\(\beta\)`. - Ej. `\(\beta:\)` "promedio de años de escolaridad en USA" -- - Un .bold[estimador] es una función - una formula - que aplicamos a los datos para obtener una *aproximación* del parámetro de nuestro parámetro de interés o *estimando*. Denotémos el estimador como `\(f(\text{datos})\)`. - Ej. `\(f(\text{datos}): \frac{\sum{\text{datos}}}{n}\)` -- - El .bold[estimado] es la cantidad obtenida al aplicar el *estimador* a los datos. Este número es una aproximación del *estimando*. Denotémoslo como `\(\hat{\beta}\)`. - Ej. `\(\hat{\beta} = 11.6\)` -- En resumen: .content-box-primary[ `$$\color{white}{\text{estimador}(\underbrace{\beta}_{\text{estimando}}): f(\text{datos}) = \underbrace{\hat{\beta}}_{\text{estimado}}}$$` ] --- ## Estimando, Estimador y Estimado .center[] --- ## Estimando, Estimador y Estimado <br> .pull-left[ ``` ## # A tibble: 100 × 3 ## year educ age ## <fct> <dbl> <dbl> ## 1 1978 12 50 ## 2 2016 13 36 ## 3 2006 20 72 ## 4 1982 9 53 ## 5 2004 16 43 ## 6 1978 16 30 ## 7 1984 15 72 ## 8 2014 16 50 ## 9 1982 16 24 ## 10 1984 12 52 ## # ℹ 90 more rows ``` ``` ## mu_hat ## 13.58 ``` ] .pull-right[ - La socióloga decide *estimar* el promedio de años de escolaridad en USA ( `\(\mu\)` ) usando la media muestral como *estimador*. - `\(\hat{\mu} = \frac{\sum \text{educ}_{i}}{n} =\)` 13.58 es nuestro *estimado* - ¿Que tanto podemos confiar en nuestro .bold[estimado] basado en esta muestra en particular? - .bold[Respuesta:] Necesitamos conocer la distribución muestral de nuestro estimador ] --- class: inverse, center, middle #Distribución Muestral de un estimador --- ##Distribución Muestral -- Si `\(\hat{\beta}\)` es un estimador definido como `\(\hat{\beta}: f(\text{datos})\)`, la **distribución muestral** de `\(\hat{\beta}\)` es la distribución de probabilidad de todos los valores posibles que `\(\hat{\beta}\)` puede tomar, calculados a partir de todas las posibles muestras de un tamaño dado `\(n\)`, tomadas de la misma población o generados por el mismo proceso. <br> -- .bold[Paso a paso,] -- - Tomamos todas las posibles muestras `\(m_{i}: \{ X_1, X_2, ..., X_n \}\)` de un tamaño dado `\(n\)`, generados por el mismo proceso (o a partir de la misma población). -- - En cada `\(m_{i}\)` aplicamos nuestro estimador y obtenemos `\(\hat{\beta}_{i}\)`. Formalmente, `\(f(m_{i}) = \hat{\beta}_{i}\)`. -- - La .bold[distribución muestral] del estimador `\(\hat{\beta}\)` refiere a la distribución de la colección obtenida de estimados `\(\hat{\beta}_{i}\)`. -- - Como toda distribución de probabilidades, la .bold[distribución muestral] indica la probabilidad de que el estimador `\(\hat{\beta}\)` tome diferentes valores. --- ##Distribución Muestral de la media muestral #### Ejemplo via Simulación Monte Carlo - La variable `\(\text{educ}\)` en la población de USA distribuye Normal con `\(\mu=12.85\)` y `\(\sigma=3.464\)`. - Tomamos 5000 muestras alesatorias de tamaño 100 a partir de esta población: `\(m_{100_i}\)` - En cada muestra calculamos la media muestral de la variable `\(X\)`: `\(\bar{X}_{100_i}\)` -- .bold[Implementación en `R`:] ``` r # población (N=un millón, media=4, sd=3) educ_poblacion <- tibble(educ = rnorm(n=10^6, mean=12.85, sd=3.464)) # simulación: resultados <- tibble(estimado = numeric(5000)) for (i in 1:5000) { # tomamos 5000 muestras de tamaño 100 muestra_i <- sample_n(educ_poblacion, size=100, replace = TRUE) # en cada muestra calculamos media y guardamos resultado resultados$estimado[i] <- mean(muestra_i$educ) } ``` --- ##Distribución Muestral de la media muestral La colección de estimados se ve así: .pull-left[ ``` ## # A tibble: 5,000 × 1 ## estimado ## <dbl> ## 1 13.01 ## 2 13.49 ## 3 13.33 ## 4 12.65 ## 5 13.12 ## 6 12.94 ## 7 12.08 ## 8 12.89 ## 9 13.00 ## 10 13.07 ## 11 13.01 ## 12 12.75 ## 13 13.42 ## 14 12.96 ## 15 12.54 ## # ℹ 4,985 more rows ``` ] -- .pull-right[ - La estimación de la media muestral es aleatorias porque las muestras son aleatorias - ¿Cómo se distribuyen estas estimaciones? <br> - El .bold[Teoréma del Límite Central] nos dice que: `$$\bar{X}_{n} \sim \text{Normal}\bigg(\mu, \frac{\sigma}{\sqrt{n}}\bigg)$$` ] --- ##Distribución Muestral La colección de estimados se ve así: .pull-left[ ``` ## # A tibble: 5,000 × 1 ## estimado ## <dbl> ## 1 13.01 ## 2 13.49 ## 3 13.33 ## 4 12.65 ## 5 13.12 ## 6 12.94 ## 7 12.08 ## 8 12.89 ## 9 13.00 ## 10 13.07 ## 11 13.01 ## 12 12.75 ## 13 13.42 ## 14 12.96 ## 15 12.54 ## # ℹ 4,985 more rows ``` ] .pull-right[ - La estimación de la media muestral es aleatorias porque las muestras son aleatorias - ¿Cómo se distribuyen estas estimaciones? <br> - El .bold[Teoréma del Límite Central] nos dice que: `$$\bar{X}_{n} \sim \text{Normal}\bigg(\mu, \frac{\sigma}{\sqrt{n}}\bigg)$$` <br> - En nuestro caso: `$$\bar{X}_{100} \sim \text{Normal}\bigg(12.85, \frac{3.464}{\sqrt{100}}\bigg)$$` ] --- ##Distribución Muestral de la media muestral .pull-left[ <!-- --> ] .pull-right[ - El .bold[Teoréma del Límite Central] nos dice que: <br> `$$\bar{X}_{100} \sim \text{Normal}\bigg(12.85, \frac{3.464}{\sqrt{100}}\bigg)$$` ] --- ##Distribución Muestral de la media muestral .pull-left[ <!-- --> ] .pull-right[ - El .bold[Teoréma del Límite Central] nos dice que: <br> `$$\bar{X}_{100} \sim \text{Normal}\bigg(12.85, \frac{3.464}{\sqrt{100}}\bigg)$$` <br> - Nuestra simulación confirma la teoría ] --- class: inverse, center, middle #Estimación Puntual --- ##Estimación Puntual .pull-left[ - Cuando contamos con .bold[UNA] muestra no tenemos una distribución de estimados - Tenemos una .bold[estimación puntual] <br> Por ejemplo: `\(\bar{X}_{100}\)` = 13.58 <br> - Sabemos que la media muestral es un estimador *insesgado* de la media poblacional (en promedio coinciden) - Sin embargo, .bold[la estimación puntal no necesariamente corresponde al parámetro poblacional]. - No nos tomamos este número TAN enserio: .bold[estimación de intervalos]. ] .pull-right[ <!-- --> ] --- class: inverse, center, middle ##Hasta la próxima clase. Gracias! <br> Mauricio Bucca <br> https://mebucca.github.io/ <br> github.com/mebucca