Tarea corta #1

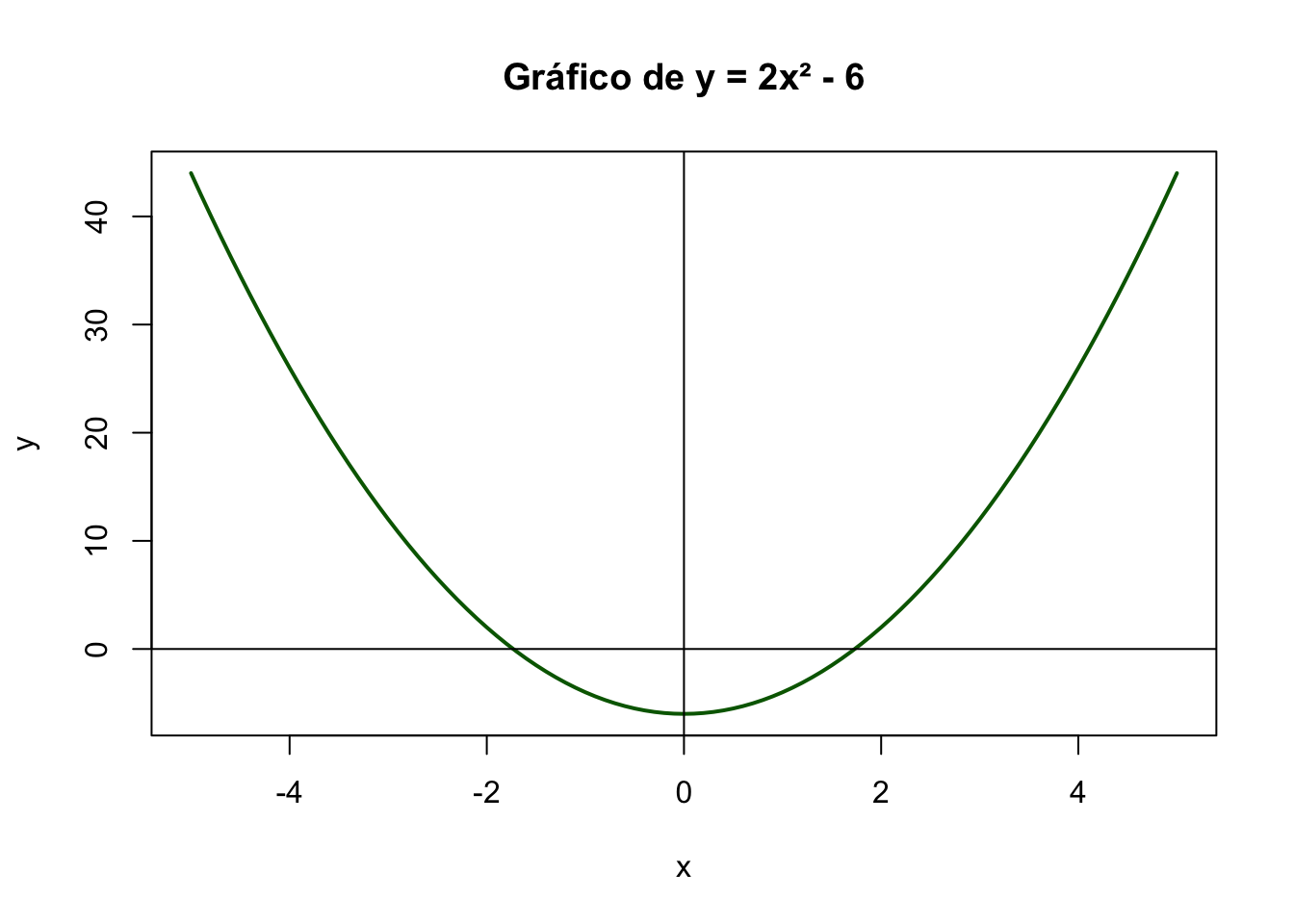
Ponderación: 5% de la nota final del curso.

1) Exponenciales y Logaritmos

1. Simplifica: \((3^2) \cdot (3^4)\)
   > Paso 1: Usa la propiedad de potencias con misma base: \(a^m \cdot a^n = a^{m+n}\)
   > Paso 2: \(3^2 \cdot 3^4 = 3^{2+4} = 3^6\)
   > Paso 3: \(3^6 = 729\)
   > Respuesta: \(3^6 = 729\)

2. Resuelve por \(x\): \(\ln(x) = 2\)
   > Paso 1: Aplica la definición de logaritmo natural: si \(\ln(x) = 2\), entonces \(x = e^2\)
   > Paso 2: \(e^2 \approx 7.389\)
   > Respuesta: \(x = e^2 \approx 7.389\)

3. Simplifica: \(\frac{e^{5x}}{e^{x}}\)
   > Paso 1: Usa la propiedad \(\frac{e^a}{e^b} = e^{a-b}\)
   > Paso 2: \(\frac{e^{5x}}{e^{x}} = e^{5x - x} = e^{4x}\)
   > Respuesta: \(e^{4x}\)

4. Simplifica: \(\ln(a) - \ln(b)\)
   > Paso 1: Usa la propiedad \(\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)\)
   > Respuesta: \(\ln\left(\frac{a}{b}\right)\)

5. Simplifica: \(\ln(\sqrt{z})\)
   > Paso 1: Expresa la raíz cuadrada como potencia: \(\sqrt{z} = z^{1/2}\)
   > Paso 2: \(\ln(z^{1/2}) = \frac{1}{2} \ln(z)\)
   > Respuesta: \(\frac{1}{2} \cdot \ln(z)\)

2) Sumatoria

Calcula la sumatoria de \((a \cdot i - b)\) desde \(i = 1\) hasta \(4\).

Paso 1: Escribe la sumatoria explícitamente:
\((a \cdot 1 - b) + (a \cdot 2 - b) + (a \cdot 3 - b) + (a \cdot 4 - b)\)
Paso 2: Agrupa los términos con \(a\) y los términos con \(b\):
\(a(1 + 2 + 3 + 4) - 4b = a \cdot 10 - 4b\)
Respuesta: \(10a - 4b\)

3) Derivadas

1. Calcula la derivada de la siguiente función: \(f(x) = 5x^3 + 2x^2 - 7x + 4\)
   > Paso 1: Usa la regla de potencias: \(\frac{d}{dx}(x^n) = nx^{n-1}\)
   > Paso 2: \(f'(x) = 15x^2 + 4x - 7\)
   > Respuesta: \(f'(x) = 15x^2 + 4x - 7\)

2. Dada la función: \(y = 2x^2 - 6\)

1. Grafica la función.

curve(2*x^2 - 6, from = -5, to = 5, col = "darkgreen", lwd = 2, ylab = "y", xlab = "x", main = "Gráfico de y = 2x² - 6")
abline(h = 0, v = 0, col = "black")

2. Identifica por inspección visual el valor de \(x\) en que la función alcanza su mínimo.
   > La función cuadrática \(y = ax^2 + bx + c\) con \(a > 0\) alcanza su mínimo en \(x = -\frac{b}{2a}\)
   > En este caso, \(b = 0\), por tanto \(x = 0\)
   > Respuesta: \(x = 0\)

3. Determina el valor de la pendiente en ese punto.
   > Derivada: \(y' = \frac{d}{dx}(2x^2 - 6) = 4x\)
   > Evaluando en \(x = 0\): \(y'(0) = 0\)
   > Respuesta: \(y' = 0\)

4) Aproximación discreta de integrales

Aproxima la integral de \(f(x) = x^2\) desde 0 hasta 2 usando 4 rectángulos. Divide el intervalo desde 0 hasta 2 en 4 subintervalos iguales y evalúa \(f(x)\) en el borde izquierdo de cada subintervalo.

Paso 1: Subintervalos: [0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2]
Paso 2: Evaluaciones: \(f(0) = 0\), \(f(0.5) = 0.25\), \(f(1) = 1\), \(f(1.5) = 2.25\)
Paso 3: Área total: \(0.5(0 + 0.25 + 1 + 2.25) = 0.5(3.5) = 1.75\)
Respuesta: 1.75

5) Integral definida

Evalúa la integral: \(\int_{0}^{2} x^2 \, dx\)

Paso 1: Usa la regla de potencias: \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\)
Paso 2: \(\int x^2 dx = \frac{x^3}{3}\)
Paso 3: Evalúa: \(\left[\frac{x^3}{3}\right]_{0}^{2} = \frac{8}{3} - 0 = \frac{8}{3}\)
Respuesta: \(\frac{8}{3} \approx 2.67\)